EFFICIENTLY SCALING TRANSFORMER INFERENCE 论文翻译(使用Claude)
详细解读可参照佳瑞老师的知乎文章
摘要
我们研究了Transformer模型高效生成式推理的问题,特别是在最具挑战性的场景下:大型深度模型、严格的延迟目标和长序列长度。更好地理解大型基于Transformer模型推理的工程权衡非常重要,因为这些模型的应用场景正在各个应用领域快速增长。我们开发了一个简单的推理效率分析模型,用于根据应用需求选择针对TPU v4切片优化的最佳多维分区技术。我们将这些技术与一系列低级优化相结合,在500B+参数模型上实现了延迟和模型FLOPS利用率(MFU)权衡的新帕累托前沿,性能优于FasterTransformer基准测试套件。我们进一步展示,通过适当的分区,多查询注意力机制(即多个查询头共享单个键/值头)较低的内存需求能够支持扩展到32倍更大的上下文长度。最后,我们在PaLM 540B参数模型上实现了:在生成阶段使用int8权重量化时,低批次大小下每个token的延迟为29毫秒;在处理输入token的大批次场景下达到76%的MFU,同时支持2048个token的长上下文长度。
1 引言
将基于Transformer的模型扩展到100B+参数(Brown等,2020;Kaplan等,2020;Rae等,2021;Hoffmann等,2022),以及后来的500B+参数(Chowdhery等,2022;Smith等,2022),已经在自然语言处理基准测试上取得了最先进的结果。这些大型语言模型(LLMs)在各种应用中的实用性使它们极具广泛使用的吸引力。虽然Transformer架构的序列并行性使其能够进行高度并行的训练,但这些模型的高效部署在实践中具有挑战性,因为生成式推理是逐个token进行的,每个token的计算顺序依赖于先前生成的token。因此,支持在数千个芯片规模上高效训练的模型,需要仔细关注并行布局和内存优化,以释放高效、低延迟推理所需的可扩展性。本文专注于一套简单的工程原则,使大规模基于Transformer的模型能够在各种具有挑战性的生产环境中高效服务。
我们考虑了大语言模型下游应用的需求。一些应用(包括聊天机器人等交互式工作负载)涉及严格的延迟约束(Thoppilan等,2022)。其他应用(包括用于评分或蒸馏的离线推理)则强调高吞吐量和低每token成本,而对延迟要求较低。
我们简要讨论是什么使大语言模型的生成式推理具有挑战性。首先,大型模型由于训练的模型参数以及解码期间所需的瞬态状态而具有巨大的内存占用。模型参数通常无法装入单个加速器芯片的内存中。每层的注意力键和值张量(我们称之为KV缓存)也必须在解码期间存储在内存中。其次,考虑到Transformer生成相对于训练的并行性要低得多,严格的延迟目标对生成式推理来说尤其具有挑战性。巨大的内存占用导致需要从高带宽内存(HBM)将参数和KV缓存加载到每步的计算核心,从而产生大量的内存流量,因此需要很大的总内存带宽才能满足给定的延迟目标。最后,注意力机制的推理成本随着输入序列长度呈二次方增长(Sukhbaatar等,2019;Choromanski等,2020;Dao等,2022)。
我们发现优化大语言模型推理效率的两个关键。首先,我们发现构建一个强大且抽象的分区框架很有用,能够在Transformer推理的有限并行性下达到模型并行扩展的极限。在这个框架内,我们针对具有特定应用需求的给定模型大小分析求解最佳分区策略。这使用户能够直观地理解权衡并选择适合其应用的最佳多轴张量分区策略、批次大小和芯片配置,而不是对分区策略进行黑盒穷举搜索(Zheng等,2022;Xu等,2021)。为了在实践中充分实现性能,我们使用了对跨芯片集合操作的额外细粒度控制和低级调度优化。其次,我们应用内存优化并充分利用PaLM的多查询注意力机制来减少不必要的张量开销,最大化在给定数量芯片上能容纳的批次大小,从而实现更高的吞吐量。
本文的主要目标是提供一套工程原则,说明如何最佳地分区模型以扩展Transformer推理。换句话说,不同分区策略的性能如何受模型大小、序列长度和硬件芯片数量变化的影响?当在延迟和吞吐量之间权衡时,最优分区策略如何变化?这些影响背后的直观和数学推理是什么?正如我们在后面章节中展示的,随着模型大小、序列长度以及延迟和吞吐量目标的应用需求变化,正确的权衡和策略也会发生变化,因此拥有一个能够轻松表达不同策略和选择的框架非常重要。
在第2节中,我们描述了用于比较不同分区策略的具体指标和权衡。在第3.1节中,我们概述了大型语言模型的分区原则。在第3节的其余部分,我们描述了几种具体的分区策略,并在第4节中对PaLM系列大型语言模型进行了实证验证。
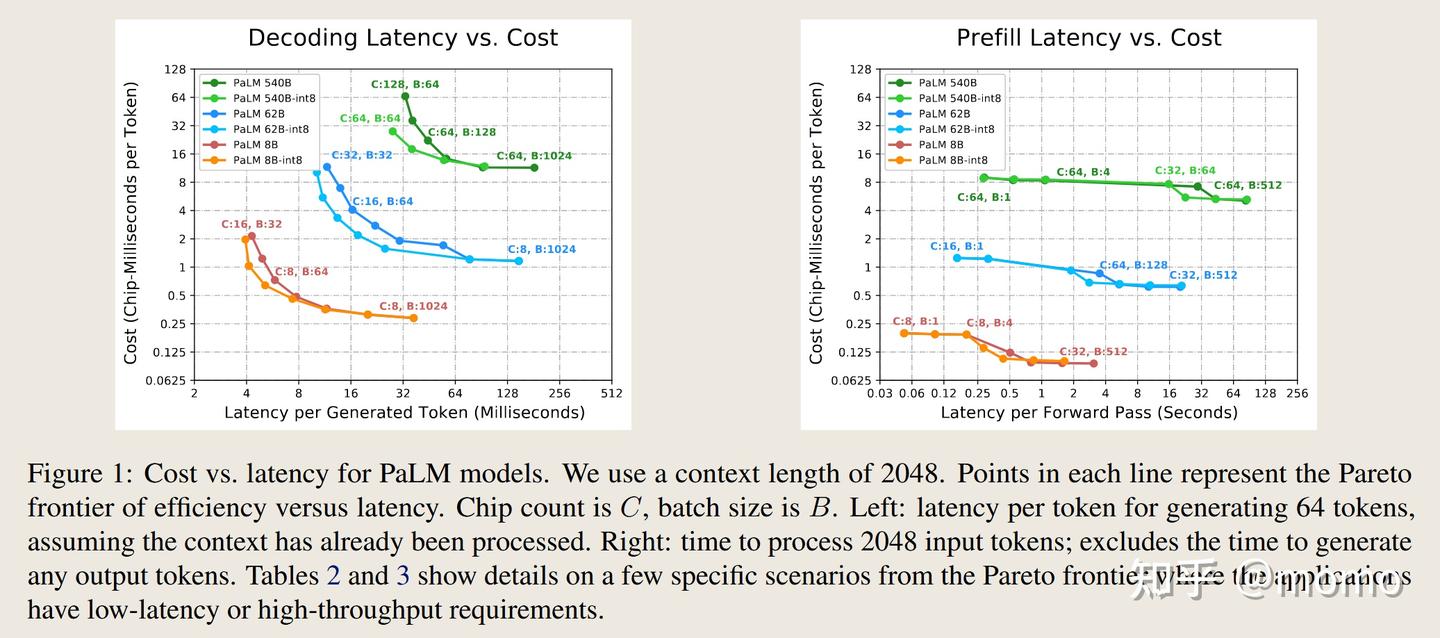
对于在64个TPU v4芯片上运行的最先进的540B参数密集模型,我们在生成期间实现了低批次大小下每token 29毫秒的延迟(使用int8权重量化),在处理输入token的大批次场景下实现了76%的MFU,同时支持2048个token的大上下文长度。图1(左)展示了我们使用PaLM模型生成文本的性能。对于在64个TPU v4芯片上使用int8权重运行PaLM 540B的交互式应用(如聊天机器人),我们的实现可以处理用户的64个token文本,查询1920个token的缓存对话历史,并在总共1.9秒内生成64个token的响应。对于面向离线吞吐量的应用,我们的实现可以处理1984个token的输入并生成64个token的输出,对于大量示例,整体FLOPS效率达到73%。表2展示了几个具体场景的更多细节。
2 推理成本权衡
扩大模型规模可以释放新的能力和应用,但在推理成本方面存在根本性的权衡。我们通过以下指标来衡量推理成本:延迟、吞吐量和模型FLOPS利用率。延迟是推理的总时间,可以分解为处理推理开始时存在的输入token所需的时间(我们称之为”预填充”)和自回归生成输出token所需的时间(我们称之为”解码”)。解码延迟也可以按”每步”来衡量,即除以每个序列中的token数量。预填充或解码的吞吐量是每秒处理或生成的token数量。模型FLOPS利用率(MFU)是观察到的吞吐量与理论最大吞吐量的比率,其中理论最大吞吐量是指基准测试的硬件设置在峰值FLOPS下运行且没有内存或通信开销时的吞吐量。
更大的模型无法装入单个加速器芯片,需要跨多个加速器芯片进行分区才能装入内存。这也使我们能够将下面描述的内存和计算成本分摊到所有芯片上,但代价是引入了芯片间通信。
内存成本。 我们在设备上的高带宽内存(HBM)中存储张量,如权重和KV缓存。虽然还有其他张量通过HBM,但它们的内存占用要小得多,因此我们只关注这两组最大的张量。这些张量需要在模型的每次前向传播(预填充或解码步骤)中从HBM传输到芯片的计算核心一次。这需要一定的时间,我们称之为”内存时间”。在小批次大小和序列长度下,加载权重的时间占主导地位。在更大的批次大小和序列长度下(例如,批次大小512+时有2048+个token),加载KV缓存的时间占主导地位。
计算成本。 一个N参数的仅解码器模型在前向传播中每个token需要2N次矩阵乘法FLOPS,因为每次矩阵乘法在前向传播中对每对输入token和参数值执行一次乘法和一次加法(Kaplan等,2020)。如果所有芯片都以峰值FLOPS运行,这些矩阵乘法将需要一定的时间,我们称之为”计算时间”。对于大型模型,注意力机制中的矩阵乘法通常每个token增加的FLOPS要少得多,通常可以忽略不计。尽管注意力的计算成本相对较小,但它仍然可以占据内存容量和带宽成本的很大一部分,因为(与权重不同)KV缓存对于批次中的每个序列都是唯一的。
2.1 预期的权衡和挑战
内存时间的权重加载部分和非注意力计算时间都与模型大小成正比,与芯片数量成反比。然而,对于给定的分区布局,芯片间通信所需的时间随着使用的芯片数量减少得较慢(或根本不减少),因此随着芯片数量的增加,它成为越来越重要的瓶颈。
我们考虑一些使这些权衡变得特别具有挑战性的场景。
如果应用需要尽可能低的延迟,我们需要使用更多芯片,并以尽可能多的方式对模型进行分区。通常可以通过较小的批次大小实现较低的延迟,但较小的批次大小也会导致较差的MFU,从而导致每个token的总成本(以芯片秒或美元计)更高。
如果应用需要生成具有长注意力上下文的文本,会大幅增加推理时间。对于使用多头注意力的500B+模型,注意力KV缓存会变得很大:对于批次大小512和上下文长度2048,KV缓存总计3TB,是模型参数大小的3倍。片上内存需要在每次生成token时从片外内存加载这个KV缓存,期间芯片的计算核心基本上处于空闲状态。
如果应用需要离线推理且延迟不是关注点,主要目标是最大化每芯片吞吐量(即最小化每token的总成本)。增加批次大小最有效,因为更大的批次通常会产生更好的MFU,但某些在小批次大小下效率不高的分区策略在批次大小增大时会变得高效。
2.2 推理设置
我们简要介绍推理设置和符号。我们考虑一个具有n_params参数的Transformer模型,在n_chips个芯片上布局进行推理。该模型具有模型(或嵌入)维度d_model(或E)、前馈中间维度d_ff(或F)和n_heads(或H)个头。
批次中每个B个序列的示例具有L_input个输入文本token,并生成L_gen个输出文本token。由于输入token在推理开始时全部存在,我们可以在所有B × L_input个token上并行运行模型,在所有token上进行单次前向传播。我们称这一步为预填充。输出token是自回归生成的,具有L_gen步的顺序循环。每一步包括通过模型的单次前向传播,之后我们为批次中的每个B个示例采样一个新token。这个循环被称为生成或解码。
由于预填充可以在L_input上并行运行,但解码必须在L_gen上顺序运行,这两个阶段具有不同的性能特征,我们分别分析它们。
3 推理效率的分区策略
我们必须将大型模型分区到多个芯片上,以便将权重和激活张量装入内存,并使计算和内存时间满足延迟要求。模型分区会在芯片之间引入通信,对于给定模型,不同的分区策略涉及不同的通信模式和通信量。在本节中,我们详细介绍了几种高级策略,用于对大型Transformer语言模型进行分区,以实现成本有效和延迟有效的推理。
3.1 分区符号和通信集合操作
我们基于具有3D环形拓扑X × Y × Z的TPU v4系统来描述本节中的分区布局。遵循(Xu等,2021),我们使用下标来指定被分区的张量维度。例如,符号BLE_xyz表示逻辑形状为BLE的张量的最后一个维度E被分成X × Y × Z个分区,其中x、y和z指的是物理TPU v4轴,每个芯片上的张量形状为[B, L, E/(X × Y × Z)]。这里B、E和F分别指批次、模型嵌入和MLP前馈维度。我们使用L来指代序列长度,并明确指定预填充或生成阶段。如果张量在轴x上被复制,则该轴在符号中被省略。我们还使用后缀”partialsum-x”来表示给定张量已在每个芯片上局部收缩(求和)(在形状中未表示的某个轴上),但在结果有意义之前仍需要跨TPU x轴上的芯片进行求和。
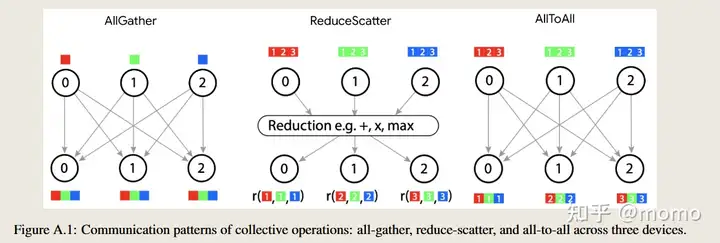
我们使用源自MPI的几个通信集合操作(Clarke等,1994)。all-reduce(x)原语对诸如BLE_yz (partialsum-x)这样的partialsum张量在环形的x轴上的芯片集合上求和,并将和广播回所有涉及的芯片,返回形状为BLE_yz的输出。出于Rajbhandari等(2020)中概述的原因,我们通常将all-reduce拆分为两个阶段:归约阶段和广播阶段。归约阶段称为reduce-scatter(x),它在x轴上的芯片集合上对BLE_yz (partialsum-x)张量求和,但产生在该轴上的芯片之间分片而不是复制的输出,布局如B_x LE_yz或BLE_xyz。广播阶段称为all-gather(x),它将张量BLE_xyz广播并连接到x轴上的所有芯片,产生比其输入大X倍的输出,在x轴上复制:BT E_yz。all-to-all集合操作将分片从一个张量维度转移到另一个维度,例如通过使用每个(源,目标)对之间的直接通信将BLH_x Q转换为B_x LHQ。图A.1说明了这些原语。
3.2 前馈层的分区
3.2.1 前馈层,1D权重固定布局
概述。 当模型无法装入单个芯片时,最简单的分区策略是1D权重固定,其中每个E × F权重矩阵沿E或F轴在n_chips个芯片之间分区(或分片)。每个权重分片在每个芯片上与相应的激活分片相乘,结果通过all-gather和/或reduce-scatter在芯片之间聚合。此外,在计算两个连续的矩阵乘法时(如在Transformer MLP块中),有一个”技巧”(Shoeybi等,2019)可以避免矩阵乘法之间的任何跨芯片通信:如果第一个矩阵乘法按输出轴分区,则每个芯片上生成的激活分片将正好是计算按输入轴分区的第二个矩阵乘法所需的那个。
随着我们在更多芯片上并行化计算,内存延迟和计算延迟确实会减少,通常接近线性。然而,无论使用的芯片数量如何,通信延迟都保持大致恒定,因为整个激活矩阵在每对矩阵乘法中都要跨芯片聚合。随着芯片数量增加,通信成为瓶颈。
细节。 我们考虑作为基线的布局,其中前馈层的权重和激活沿d_ff维度在n_chips上分区,如Megatron (Shoeybi等,2019)中所示。图2(a)显示了这种情况的分区布局。在TPU v4的3D环形拓扑上,权重的分区布局为EF_xyz和F_xyz E,即它们被分成X × Y × Z = n_chips个分区,在物理TPU轴上有X、Y和Z个分区。权重在每个芯片中保持固定,激活在芯片之间传输以匹配权重布局,需要一次all-gather和一次reduce-scatter。
在这种1D权重固定分区策略中,每个芯片在reduce-scatter和all-gather中分别获得形状为BLE的输入和输出。我们在附录A.1中推导了这些操作的通信成本。得到的通信时间为
\[T_{comm} = 2BLE / {network bandwidth}\]3.2.2 前馈层,2D权重固定布局
概述。 对于更多数量的芯片,一种更经济的策略涉及沿E和F轴对每个E × F权重矩阵进行分区,使每个分片大致为正方形。例如,如果E = 1024,F = 4096,n_chips = 64,那么我们将在E中分4路,在F中分16路,这样64个芯片中的每一个都存储权重矩阵的256×256块,激活在芯片之间传输。这称为2D权重固定。总计算成本与1D权重固定相同,但通信效率高得多:当通过一组连续的权重矩阵乘以激活矩阵时,我们可以在每次乘法之间交替在两个轴上执行激活聚合。通过正确的分区,每个芯片将始终拥有必要的激活分片来与其权重分片相乘,而无需拥有激活张量的完全复制副本。由于每个轴被分区为O(√n_chips),通信时间按O(1/√n_chips)缩放,而不是保持恒定。这意味着即使2D布局在某个芯片数量和批次大小下受通信限制,我们也可以通过添加更多芯片来继续减少延迟,因为通信时间继续减少。
然而,虽然1D权重固定”技巧”只需要我们在d_model维度上聚合,但2D权重固定需要在d_model和d_ff维度之间交替聚合。因此,当√n_chips > d_ff/d_model时,2D权重固定变得更具通信效率。由于通常d_ff = 4d_model,这发生在n_chips > 16时。
细节。 图2(b)显示了分区布局。而1D权重固定布局以每芯片未分片形状BLE运行其all-gather和reduce-scatter,此2D权重固定布局对d_model进行分区,使d_ff分区的通信量从BLE减少到BLE/X。这是以引入第二对reduce-scatter和all-gather操作为代价的,其成本必须与现有通信平衡。
权重的分区布局为E_x F_yz,即它们沿d_model维度分成X个分区,沿d_ff维度分成Y × Z个分区,其中X × Y × Z = n_chips。输入激活的分区布局与上一节相同。请注意,我们再次在芯片上保持分区权重固定,但由于它们的2D布局,激活通信包括两个all-gather和reduce-scatter。
我们在附录A.2.1中推导了最小化总通信时间的X、Y和Z的最优值。假设d_ff = 4 × d_model,我们通过X = 0.5 × √n_chips和YZ = 2 × √n_chips实现最小通信时间。得到的总通信时间为:
\[T_{comm} = 8BLE / (\sqrt{n_{chips}} × network bandwith)\]3.2.3 前馈层,权重聚集布局
概述。 在前面描述的权重固定策略中,每个芯片在内存中存储每个权重矩阵的一个分片,并且该芯片负责将其”固定”权重分片与每个相应的激活分片相乘。然后,每个芯片矩阵乘法的输出必须在芯片之间聚合,以用作后续操作的输入。
然而,随着批次大小(和序列长度)增大,输出激活的大小可能会显著大于权重的大小。当这种情况发生时,将激活保持在每个芯片上固定,而在芯片之间传输权重可能更经济。对于非常大的批次大小,最好在顺序矩阵乘法之间保持激活完全固定,要求我们在所有芯片之间完全传输权重。我们称这种方法为XYZ-权重聚集。对于中等批次大小,使用”混合”方法是有益的,其中权重和激活都沿不同轴部分传输。我们将这些方法称为X-权重聚集和XY-权重聚集。
细节。 图2(c)显示了XY-权重聚集布局。我们选择的特定布局的一个关键方面是权重以与2D权重固定相同的E_x F_yz布局开始,这样我们可以对权重聚集(在预填充期间)和权重固定(在解码期间)使用相同的权重布局。就在einsum之前,权重张量在X和Y轴上进行all-gather,通信量为EF/Z。这相对于权重固定布局是额外的通信,但作为回报,我们减少了激活的通信:跳过了一对激活的reduce-scatter/all-gather,另一对的通信量从BLE/X降至BLE/XY。
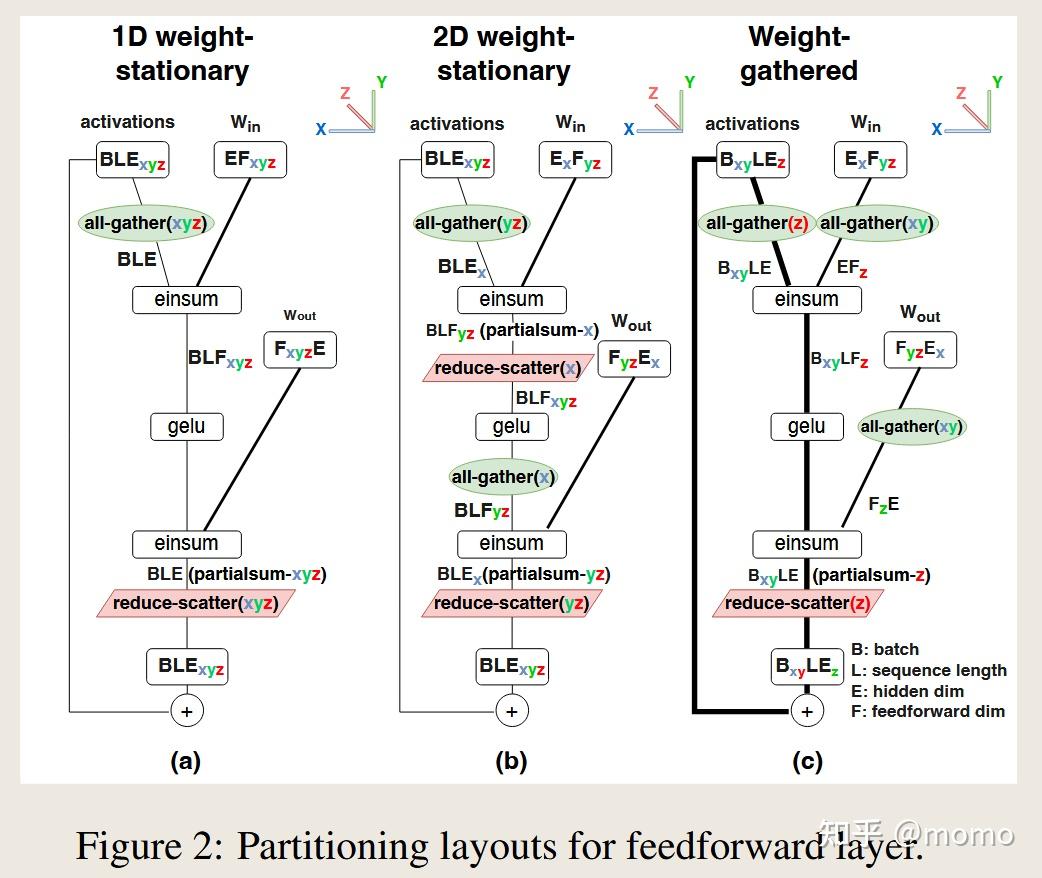
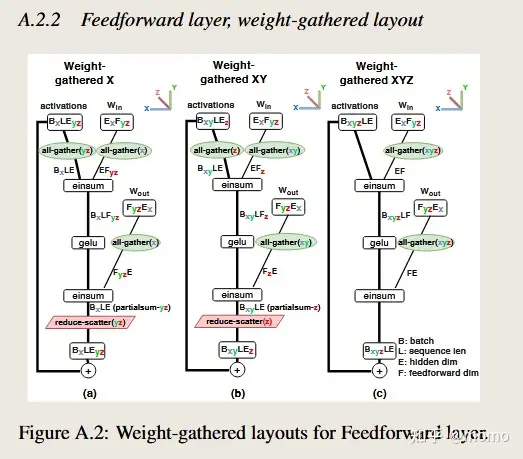
通过改变X、Y和Z轴的相对大小,我们可以权衡权重通信与激活通信,从而最小化总通信量。但我们选择在权重固定和权重聚集布局之间共享权重,这意味着我们需要匹配为权重固定布局做出的X、Y和Z的选择。我们所做的是在几个权重聚集布局的变体之间进行选择。图2(c)中显示的变体对权重使用all-gather(xy),对激活使用B_xy LE_z分区。我们的其他变体对权重使用all-gather(x)或all-gather(xyz),相应地对激活使用B_x LE_yz或B_xyz LE分区。图A.2显示了三种权重聚集布局。
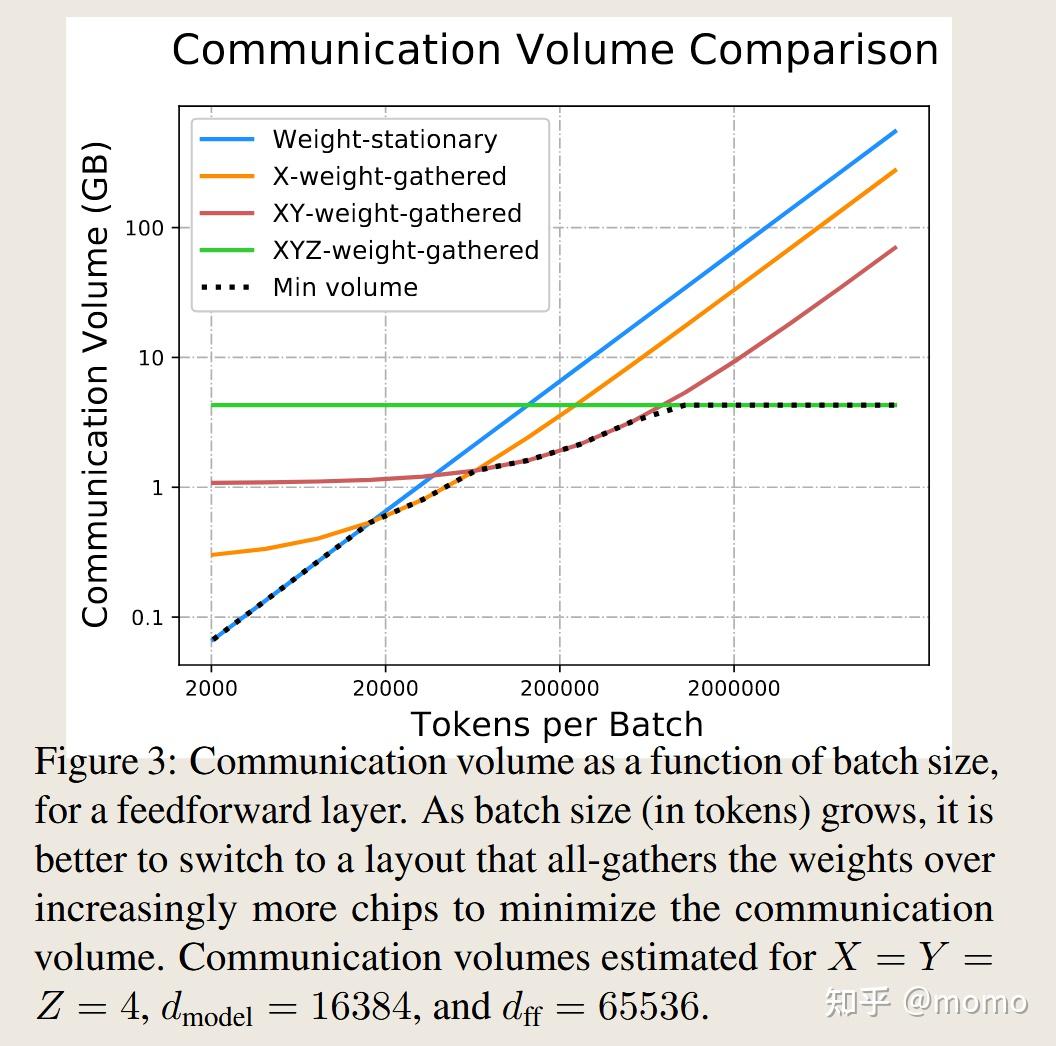
图3显示了随着批次大小增长,通信最优配置如何在这些布局之间切换——虽然2D权重固定策略在每批次token数较低时最小化通信,但不同的权重聚集布局在每批次token数较大时是最优的。这突出了根据应用目标选择不同推理配置的重要性。
我们现在展示权重聚集布局的渐近缩放。设N为权重被all-gather到的芯片数量:在X-权重聚集中N = X,在XY-权重聚集中N = XY,在XYZ-权重聚集中N = XYZ。通过选择N = √(BLn_chips/F)来最小化总通信,我们在附录A.2.2中推导了这一点。总通信时间为
\[T_{comm} = 4E\sqrt{BLF} / (\sqrt{n_{chips}} × network bandwith)\]注意BL对应于以token为单位的总批次大小。权重固定布局的通信时间与BL成线性关系,而权重聚集布局的通信时间与√BL成线性关系。因此,当批次大小和预填充序列长度足够大时,权重聚集布局变得更便宜。
3.3 注意力层的分区
多头注意力基本上可以用与前馈层相同的方式并行化,n_heads替代d_ff。但是使用多头注意力的推理会产生显著的内存容量和带宽成本来存储和加载KV缓存,这些成本在大批次或长上下文长度时可能主导推理的其余部分。
一种替代方法称为多查询注意力(Shazeer,2019;Chowdhery等,2022),仍然为查询张量发出n_heads个头,但键和值张量只有单个头。这个键和值头在n_heads个查询头之间共享。这将KV缓存张量的大小减少了n_heads倍,从而减少了加载它们的内存时间。但它也移除了一个原本用于并行性的轴,因此KV缓存和相关计算需要以不同方式分区。
分区策略。 关键设计考虑是最小化重复加载KV缓存的内存时间,这主导了推理成本。具有n_heads维度的投影矩阵(多查询注意力中的W_Q和W_O,以及多头注意力中的这两个加上W_K和W_V)的分区布局应该与前馈层中使用的布局相匹配。
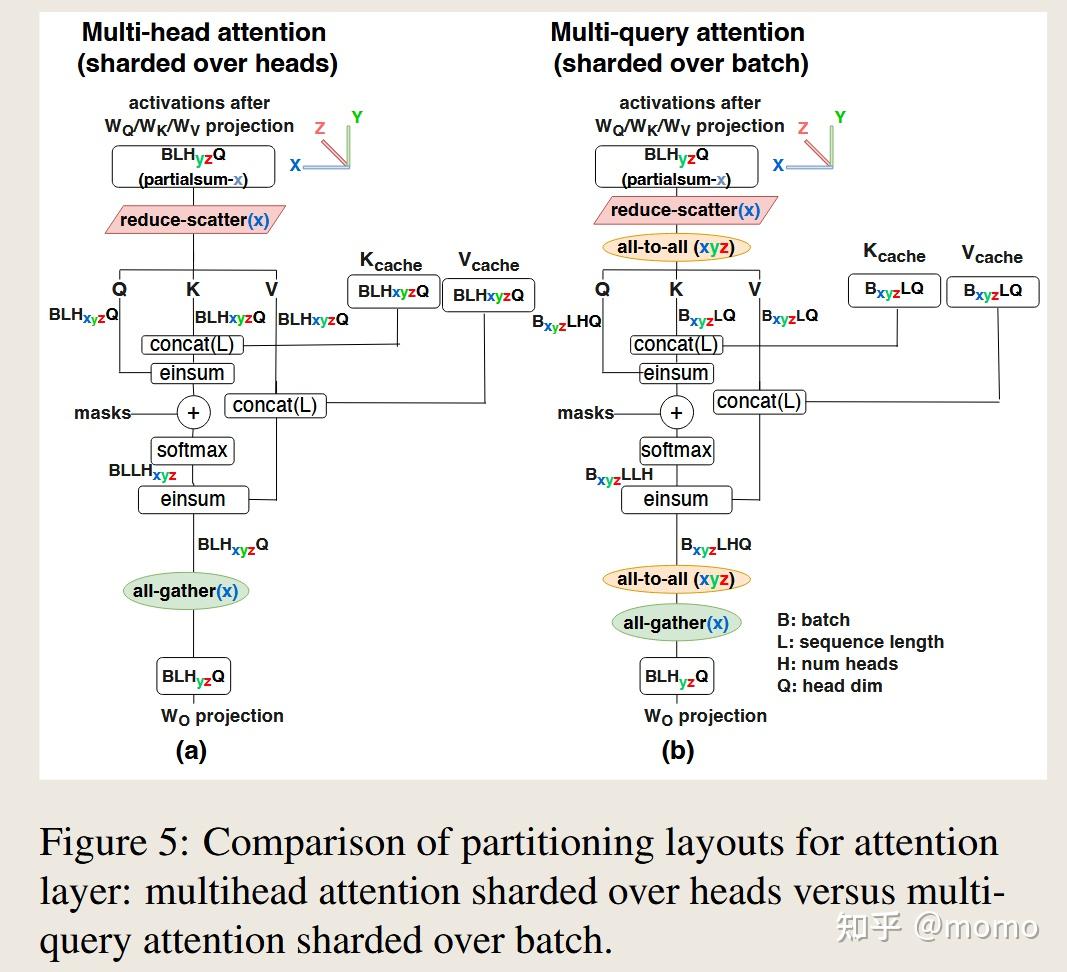
图4(a)显示了多头注意力的典型分区布局,与2D权重固定前馈布局相匹配。这里当n_heads是n_chips的倍数时,Q、K和V激活在n_heads维度上被分成n_chips个分区。对于大于n_heads的n_chips,注意力头被部分复制。多查询注意力最相似的分区布局(如图4(b)所示)以与多头注意力相同的方式处理KV缓存。即使键和值张量在所有头之间共享,它们也必须在每个芯片上复制,多查询注意力的内存成本节省就会丢失。
我们提出了一种多查询注意力的分区策略,其中Q、K和V矩阵在批次B维度上被分成n_chips个分区。图4(c)显示这将每芯片加载KV缓存的内存成本减少了n_chips倍,从而将内存时间减少相同倍数。与图5(a)中所示的多查询注意力分片策略相比,所提出的分区策略会产生额外的通信成本,即使用all-to-all集合操作重新分片输入激活张量,如图5(b)所示,其中Q、K和V矩阵在头维度上分区。
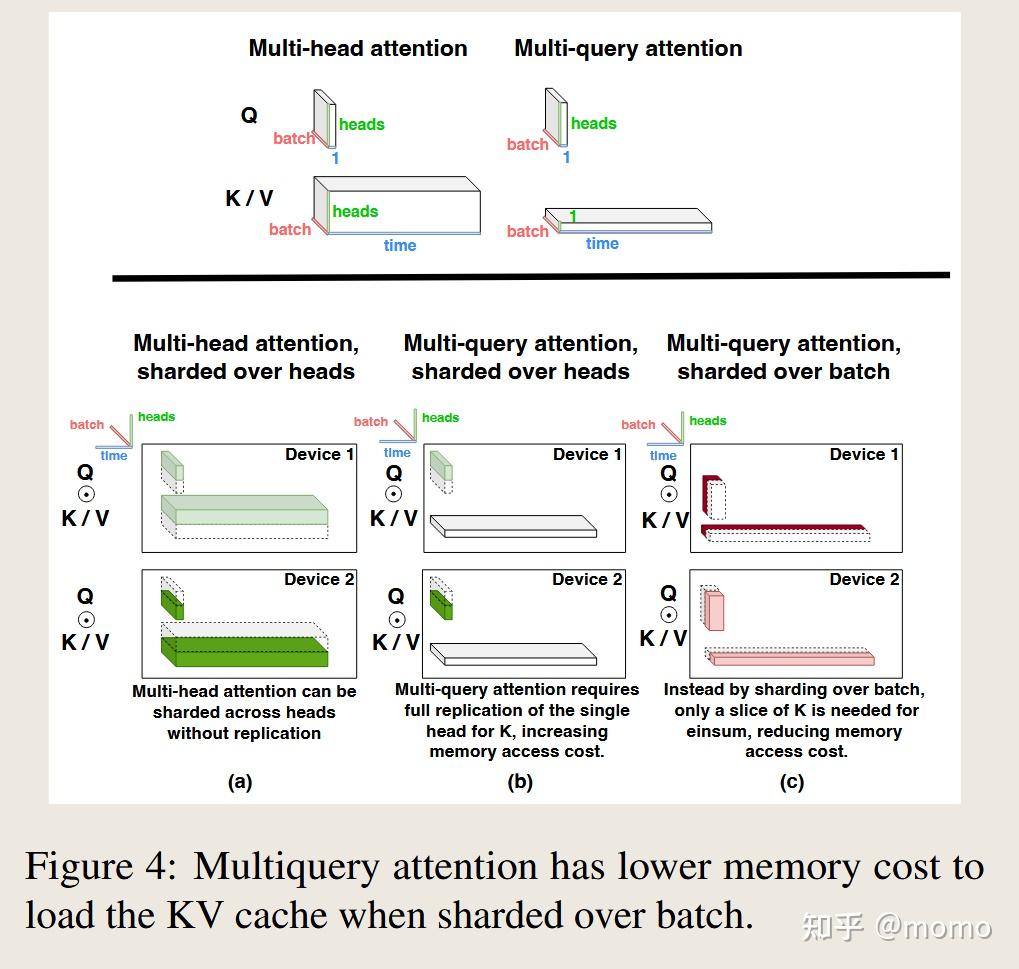
在自回归生成期间,每个示例只有一个Q、K和V张量的token,而KV缓存有许多(可能2048个)token。由于KV缓存比Q、K和V张量大几个数量级,因此在小张量上花费all-to-all通信时间来节省大张量上的内存时间是非常有利的。
在预填充期间,在批次上分片注意力通常不划算。Q张量有许多(可能2048个)token,所有这些token都针对相同的K和V张量进行查询。K和V张量的内存加载在Q张量中的所有token上摊销,因此这种内存加载通常不是预填充期间的瓶颈。因此,对于预填充,我们使用头分片布局。
通过所提出的分区布局,多查询注意力能够使用更大的批次大小和序列长度,从而除了减少内存时间带来的延迟减少外,还增加了吞吐量。如第4.2节所示,与多头注意力相比,节省了一个数量级。
3.4 并行注意力/前馈层
我们讨论PaLM(Chowdhery等,2022)中使用的每个Transformer块的”并行”公式,而不是标准的”串行”公式带来的推理延迟增益,其中前馈层和注意力层从层归一化输入并行计算并求和以获得输出。
并行公式的好处如下。首先,每层只有一个层归一化而不是两个,这在小批次大小时减少了延迟。其次,前馈层的输入矩阵可以与注意力层的查询投影矩阵W_Q融合,注意力层中的键/值投影矩阵W_K和W_V可以融合,前馈层的输出矩阵可以与注意力层的输出投影矩阵W_O融合。这种融合导致更高的FLOPS利用率,因为更大的矩阵乘法在加速器上运行得更有效。更重要的是,它还消除了每个Transformer层中d_ff/n_heads并行性所需的两个all-reduce操作之一,将该轴上的通信时间减半。
3.5 低级优化
我们使用Wang等(2023)的Looped CollectiveEinsum技术来并发运行通信和计算。这使我们能够部分或完全隐藏图2和图5中大多数reduce-scatter和all-gather操作的通信时间。对于图2和图5中的所有reduce-scatter操作,我们可以选择是reduce-scatter到批次或序列维度(B或L),还是到隐藏维度(E或F)。我们选择了后者,因为它为Looped CollectiveEinsum提供了更有效的机会,而Korthikanti等(2022)选择了前者,以避免层归一化中的通信。
CollectiveEinsum循环占推理延迟的绝大部分,因此我们投入了相当大的努力来最大化它们的性能。首先,我们使用Wang等(2023)的底层”async CollectivePermute” API开发了一套CollectiveEinsum概念的变体,以针对不同场景进行优化:延迟与吞吐量,不同数量的环形轴,与不同输入/输出集合操作融合。其次,我们明确地将通信集合操作与应该融合的矩阵乘法匹配起来,以最大化重叠的潜力。通过这些优化,我们实现了比我们开始使用的更简单的编译器分区和调度实现大约1.4倍的性能提升。如果没有这些优化,一些权重聚集布局会耗尽内存。
我们还包括了以下低级优化:更好的张量内存布局以最小化矩阵乘法期间的填充和复制,用于解码采样的更快top-k/top-p实现,Softmax和Swish的更快log-base-2实现,以及支持预填充期间序列的增量处理(FasterTransformer)。
3.6 量化
我们使用AQT库(Lew等,2022)通过将16位权重转换为int8来减少内存成本,而不会出现明显的质量损失。这使得权重加载的内存时间节省,这在低批次大小情况下特别有帮助,并且它减少了权重聚集布局中的通信量。我们尚未实现激活量化(Abdolrashidi等,2021),但我们希望它可以减少大批次配置中的计算时间,并减少权重固定布局中激活的通信量。
4 PaLM模型案例研究
方法论 我们现在对PaLM系列模型(Chowdhery等,2022)进行实证研究,选择该模型是因为其架构包含了多查询注意力和并行注意力/前馈层的技术。
我们的推理框架基于JAX(Bradbury等,2018)和XLA(XLA,2019),我们最初的高级实现基于T5X(t5x,2021)。我们的基准测试使用多达256个TPU v4芯片(Google,2022)。每个TPU v4芯片可以以275 TFLOPS运行bfloat16矩阵运算,具有32 GiB高带宽内存(HBM),带宽为1200 GB/s,并在3D环形拓扑中具有270 GB/s的互连带宽(TPUv4)。
对于PaLM 540B模型,我们将注意力头的数量从48填充到64,以便在64+个芯片上更有效地分区。这为模型增加了18B参数,代价是3%的MFU成本,但通过能够更有效地分区而获得了更多的收益。
4.1 前馈层分区
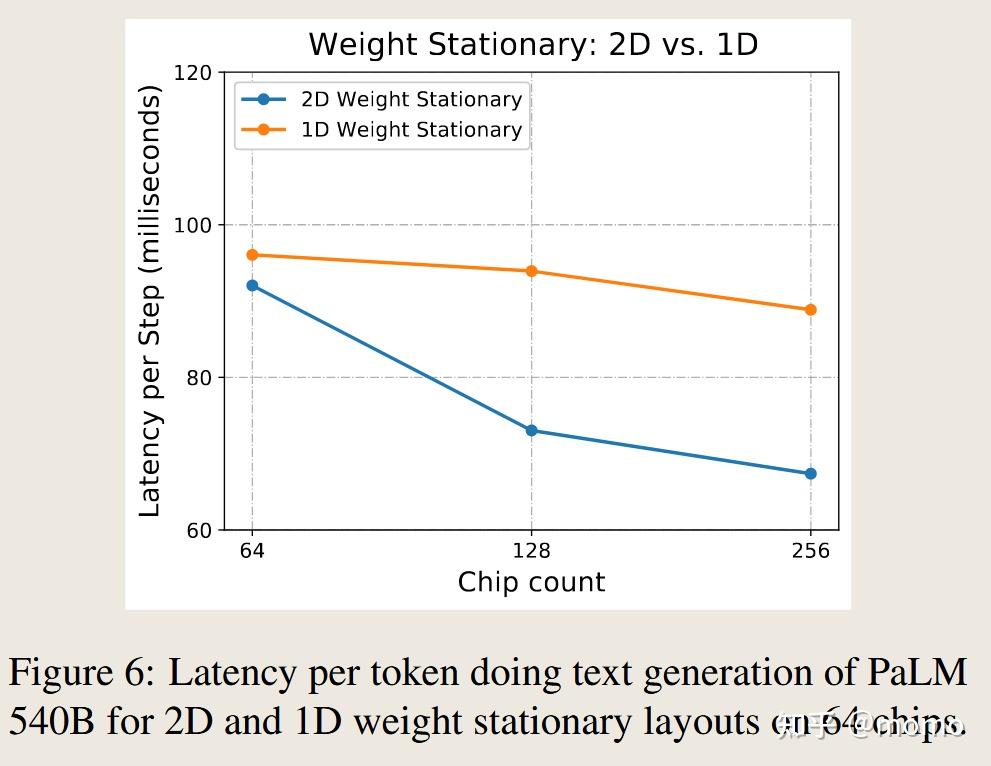
我们评估前馈层分区策略的相对性能。首先我们评估解码的性能。我们使用批次大小512来平衡延迟和MFU。图6显示了随着芯片数量增加,1D和2D权重固定布局的性能。两种布局都开始受到通信限制,但2D布局表现更好,因为其芯片数量的渐近缩放更优。
接下来我们考虑预填充阶段。我们考虑从2048个token(1个示例,2048个token)到100万个token(512个示例,每个示例2048个token)的批次大小。图7显示,最优分区布局随着批次大小的增加从2D权重固定布局切换到权重聚集布局。权重聚集布局在低批次大小时效率低下,但最终在高批次大小时变得最有效,当通信开销几乎可以忽略不计时实现76%的MFU。如果没有多查询注意力,如第4.2节所示,如此大的批次大小会因内存耗尽而失败。这突出了根据应用场景和目标使用不同选择配置推理系统的灵活性的重要性。
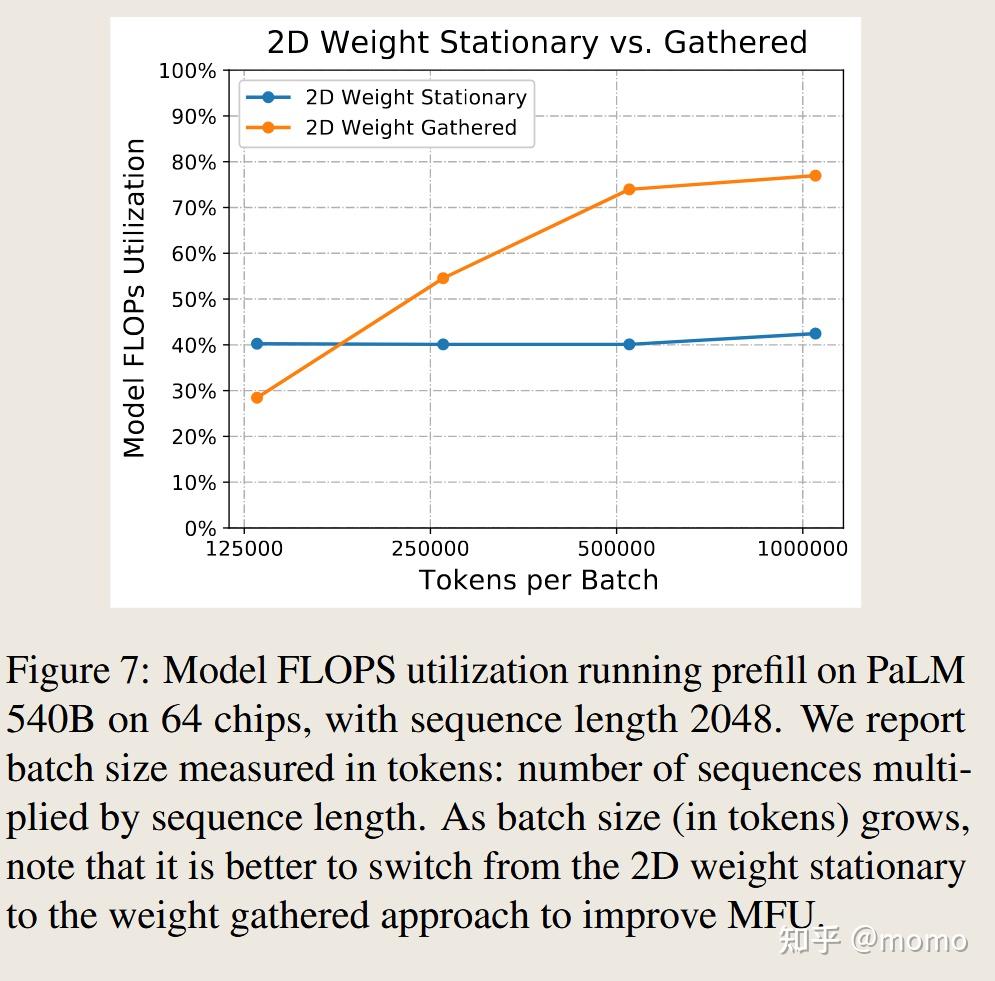
这些结果为我们提供了选择分区布局的基本策略:在预填充阶段,我们根据批次中当前的token数量从权重固定和权重聚集布局中选择。在生成阶段,我们选择2D权重固定布局,因为以token为单位的批次大小总是很小。
4.2 注意力层分区
我们现在评估第3.3节中提出的多查询注意力的分区布局。我们考虑同时使用基线布局(按注意力头分区)和优化布局(按批次分区)的多查询注意力PaLM。我们还创建了PaLM 540B的修改变体,使用多头注意力而不是多查询注意力。为了保持注意力层中的参数数量不变,我们将多查询变体中的d_head从256缩小到多头变体中的128。
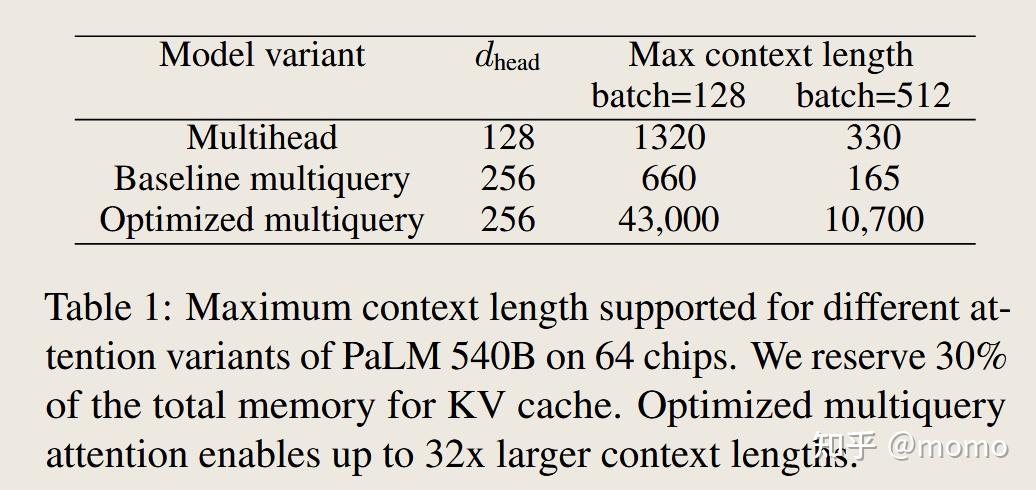
在大批次大小和上下文长度下,KV缓存可能变得非常大,使我们面临内存耗尽的风险。表1显示,优化的多查询布局可以容纳比多头和基线多查询变体长32-64倍的上下文长度。
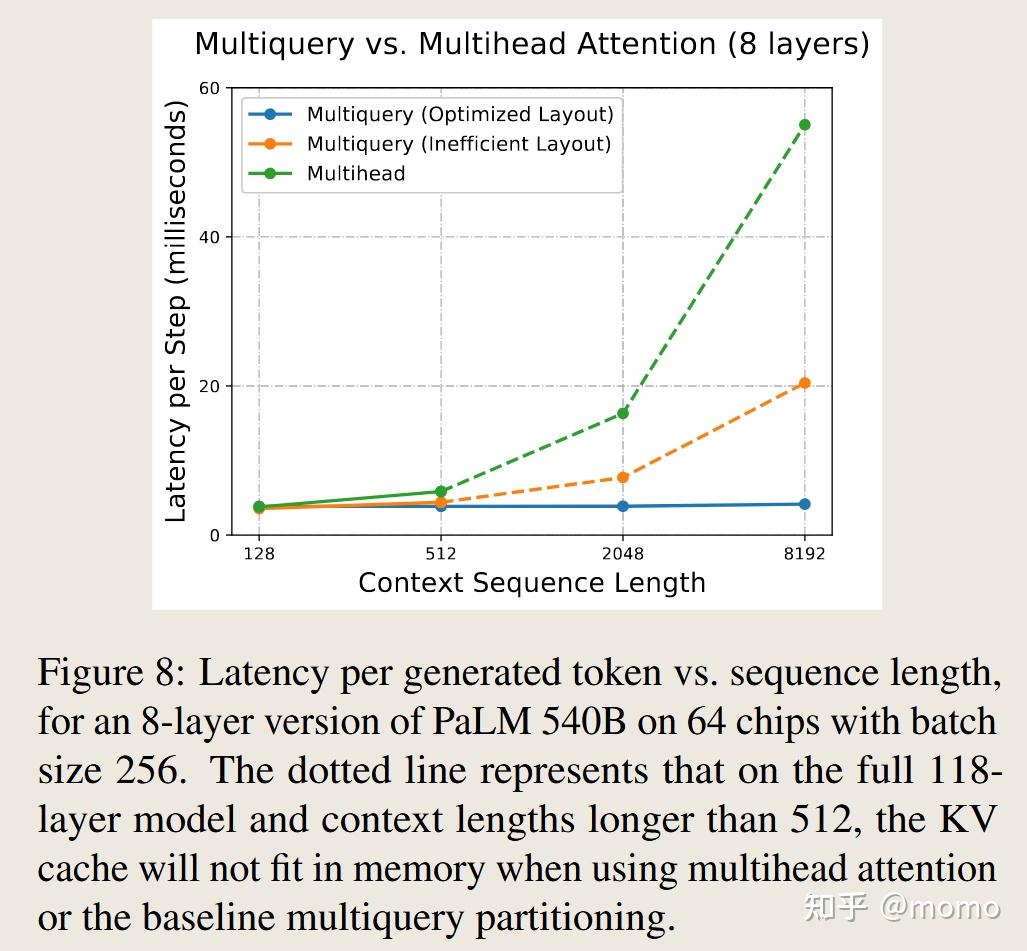
在预填充期间,多查询和多头注意力产生相似的推理延迟,因为我们并行计算许多注意力查询,注意力计算在注意力矩阵乘法上变得受计算限制。在生成期间,图8显示优化的多查询布局提高了速度。当上下文长度较短时,速度提升很小,因为几乎所有时间都花在前馈层上。随着上下文长度增长,在注意力层中加载KV缓存的时间占总推理时间的比例越来越大。多查询注意力可扩展到8192-32,768个token的序列长度(批次大小分别为512和128),注意力仅占总运行时间的8-31%。
4.3 并行注意力/前馈层
我们考虑PaLM 540B的一个变体,将Transformer块的并行公式替换为串行注意力/前馈层。在生成期间,我们使用2D权重固定布局、64个芯片和批次大小512。串行公式比并行版本的每步推理延迟高14%,因为激活的通信时间增加了。在预填充阶段,这种差异缩小了,因为权重聚集布局产生的激活通信较少。
4.4 PaLM的端到端结果
我们找到了随着PaLM系列模型规模扩展时效率和延迟之间的帕累托前沿:8B、62B和540B,权重采用bfloat16或int8。我们使用上下文长度2048,并扫描批次大小和芯片数量。
为了在不同芯片数量和批次大小的多个模型大小之间有意义地比较吞吐量,我们以每token的芯片秒成本来报告推理成本,计算公式为
成本(每token的芯片秒) = n_chips × 时间 / BL
这与运营成本成正比,与MFU成反比。
图1(左)显示了在帕累托前沿最优批次大小、芯片数量和分区策略下,生成阶段中模型大小、延迟和成本之间的关系。最低成本是在批次大小大于约512时实现的,此时成本与参数数量成正比。当我们减少批次大小时,我们改善了延迟但产生了更高的每token成本。生成的最小延迟比批次512延迟低3倍。
我们观察到int8权重量化在图1(左)中实现了最小延迟:例如,在PaLM 540B上,我们在批次大小64时使用int8权重实现了28.5ms/token,而使用bfloat16权重实现了36.9ms/token。在低延迟目标下,成本提高了刚好超过2倍,因为低批次成本由权重加载时间主导。在大批次大小下,int8和bfloat16之间的成本更为中性,因为大批次成本由计算时间主导,矩阵乘法仍然使用bfloat16运算。我们相信将激活量化为int8可以实现进一步的成本改善。
图1(右)显示了预填充阶段中模型大小、延迟和成本之间的关系。批次大小和延迟之间的权衡在预填充阶段不如生成阶段严重,甚至批次大小1也以相当低的成本运行。此外,批次512预填充的成本比批次512生成低2倍,因为我们在预填充期间使用的权重聚集布局的MFU更高。关于模型大小和MFU之间关系的更多细节在图C.1和附录C中呈现。
表2和表3显示了图1的帕累托前沿中一些关键配置,分别在PaLM 540B和PaLM 62B上。在低延迟场景中,我们将批次1预填充与批次32-64解码相结合:批次大小1在预填充阶段实现最佳延迟,但对于生成阶段,我们可以将批次大小增加到64而延迟影响可忽略不计,这样做对生成MFU显著更好。这种批次大小的混合在实践中是可能的,既可以通过从相同输入文本生成多个样本,也可以通过将批次1预填充服务器流水线化到批次64解码服务器中。
在表2和表3的高吞吐量场景中,我们使用更大的批次大小,并在预填充和解码之间切换分区布局。我们对高吞吐量场景使用bfloat16权重,因为在大批次大小下权重加载时间不重要,并且我们的软件在大批次int8模式下缺少一些优化。
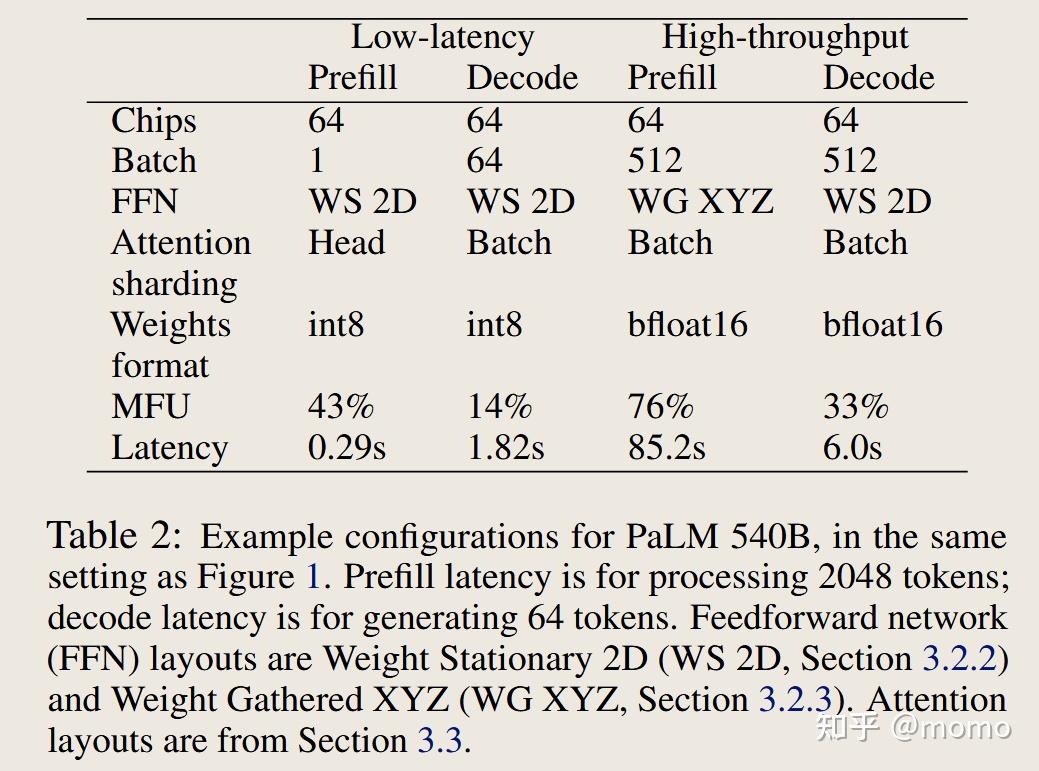
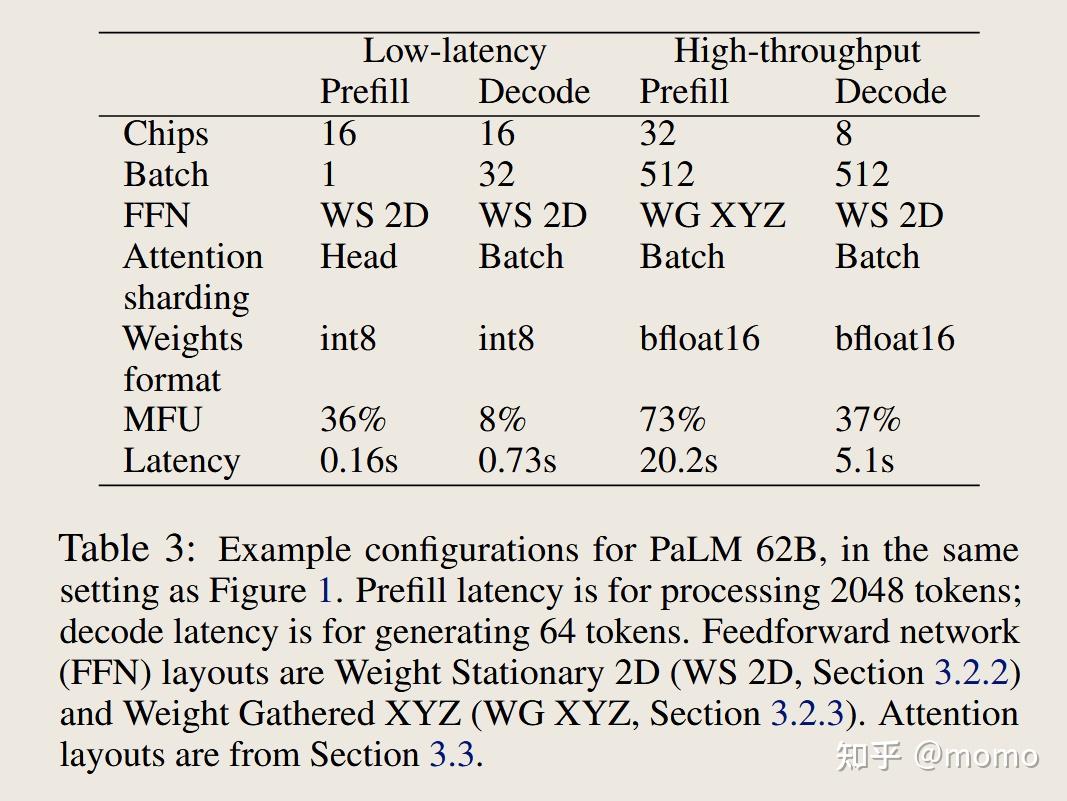
比较62B(表3)与540B模型(表2),我们发现540B模型使用更多芯片,但批次大小相似,并且使用相同的分区布局。高吞吐量MFU在模型大小之间相似。低批次延迟随着模型大小呈次线性增长:即使更大的模型从内存加载成比例更多的权重,在受通信限制之前我们可以将它们分区到更多芯片上。基于图1(左),我们估计模型大小和延迟之间存在大约平方根关系。
5 FASTERTRANSFORMER基准测试
我们现在将我们的实现与FasterTransformer基准测试在各种批次大小以及预填充和生成配置下进行比较。我们的基准测试设置与FasterTransformer基准测试之间存在多个差异。特别是,我们使用不同类型的芯片和芯片数量——FasterTransformer使用16-32个具有80GiB HBM的NVIDIA A100,而我们使用64个具有32GiB HBM的Google TPU v4芯片。因此,我们以MFU来报告吞吐量数据,这对芯片数量和芯片FLOPS都进行了归一化。
图9显示了我们的实现相对于三种FasterTransformer配置的性能。我们对Megatron 530B模型(Smith等,2022)和大小相似的PaLM 540B模型进行基准测试,后者具有架构优化,包括多查询注意力和并行注意力/前馈层(表D.1中的完整差异列表)。我们的PaLM 540B实现达到了最佳的绝对延迟,并且我们的实现在除一个延迟目标外的所有延迟目标下也为Megatron模型提供了最佳的MFU。在此基准测试中,我们的PaLM实现比Megatron实现的MFU高出多达10%,主要是因为并行注意力/前馈层。与第4.2节相比,并行层的优势被Megatron更大的d_model和d_ff大小部分抵消了。在此基准测试中,多查询注意力的优势不明显,因为注意力上下文长度太短。
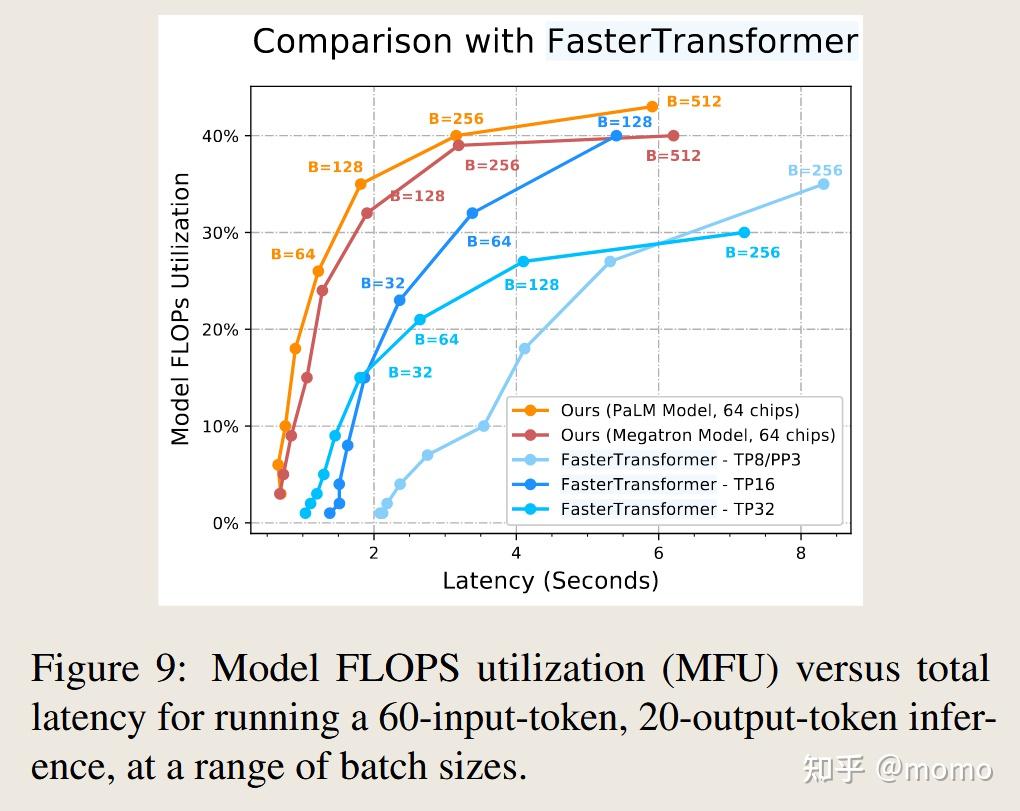
FasterTransformer报告了8路、16路和32路张量并行的结果。他们的32路张量并行在所有报告的基准测试中最高达到33%的MFU,而在16路张量并行配置中为46%的MFU。这可能表明在超过这一点扩展张量并行存在通信瓶颈。相比之下,我们的实现能够扩展到64路张量并行,同时仍然实现44%的MFU,这表明我们的2D权重固定分区策略在TPU v4更大的高速互连域上具有优越的可扩展性。
我们在附录D中提供了FasterTransformer基线中使用的所有配置的结果。我们还注意到,我们在整篇论文中的基准测试试图包含更具挑战性的推理场景,例如1024-4096范围内的上下文长度,并分别报告生成阶段和预填充阶段的推理延迟(因为它们具有不同的特征)。
6 相关工作
并行方法。 先前的工作提出了几种高效分区方法来有效训练大型模型,例如NeMo Megatron(Korthikanti等,2022)、GSPMD(Xu等,2021)和Alpa(Zheng等,2022)。FasterTransformer为一系列不同模型大小(包括Megatron-Turing NLG 530B)建立了多GPU多节点推理的基准测试套件。关键的推理加速来自于结合张量并行和流水线并行以及内存优化。DeepSpeed Inference(Aminabadi等,2022)进一步启用ZeRO offload,除了GPU内存外还使用CPU和NVMe内存。对于更大的批次大小,EffectiveTransformer将连续序列打包在一起以最小化填充。Zheng等(2022)通过整数线性规划泛化了并行策略的搜索。相比之下,本文基于直观的、有实证支持的分析权衡来推导分区策略,以满足应用需求,这些策略在模型大小、上下文长度和芯片数量上都能很好地扩展。
机器学习推理效率。 几种提高Transformer模型推理效率的方法(Gupta和Agrawal,2020)关注于模型架构改进,例如高效注意力层(Roy等,2020;Choromanski等,2020;Kitaev等,2020;Sukhbaatar等,2019;Child等,2019)、蒸馏(Sanh等,2019;Sun等,2020)和模型压缩技术,如剪枝(Li等,2020b;Brix等,2020;Zhou等,2021;Li等,2020a;Wang等,2020)或量化(Dettmers等,2022;Abdolrashidi等,2021;Zafrir等,2019;Zhang等,2018)。本文重用了先前关于模型量化的工作以增加推理加速,我们描述的技术也可以与其他模型压缩方法结合使用。
7 结论
大型基于Transformer的模型正在多个领域释放新的能力和应用,但随着模型规模的扩大,我们需要重大进展来实现其访问的民主化。本文研究了Transformer推理工作负载的扩展特性,并提出了实用的分区方法来满足具有挑战性的应用需求,例如严格的延迟目标(对于500B+参数模型,延迟在秒级)。我们表明,最佳延迟是通过远远超越传统的单服务器推理范式,将推理扩展到64+个芯片来实现的。更长的上下文长度会产生更高的内存成本,但具有适当分区的多查询注意力降低了这一成本,使长上下文推理变得实用。所提出的分区策略可以泛化到许多拓扑,包括GPU系统中的单节点和多节点NVLink网络。
尽管我们实现了将推理工作负载的规模扩展到极限的目标,但我们观察到FLOP数量和通信量从根本上限制了密集Transformer模型的推理性能。稀疏性技术,如基于任务的专家混合架构(Fedus等,2022;Kudugunta等,2021;Lepikhin等,2020;Shazeer等,2017),以及为每个输入和生成时间步分配不同计算量的自适应计算技术(Jaszczur等,2021;Schuster等,2022),有望减少Transformer模型的每token FLOP数。我们希望这些减少每token FLOP数的技术,以及压缩芯片间通信的技术,将在成本和延迟方面实现进一步的提升。
附录 A 分区策略:推导通信成本
A.1 all-gather/reduce-scatter的成本
图A.1显示了我们在分区策略中使用的典型集合操作及其在三个设备上的通信模式。对于K个分区上的all-gather,其中每个芯片产生大小为D的输出,通信模式需要在(K-1)个互连链路上传输大小为D/K的块,以将其复制到(K-1)个芯片。all-gather的结果通信时间为
\[T_{\text{comm(all-gather)}} = \frac{D}{\text{网络带宽}} \cdot \frac{K-1}{K}\]这是一个通用的成本模型,适用于大多数实际网络拓扑(Chan等,2007),不仅仅是TPU的环形拓扑。
reduce-scatter的通信时间 $T_{\text{comm(reduce-scatter)}}$ 相同,只是D是(较大的)输入缓冲区的大小而不是(较小的)输出缓冲区的大小。因此,all-reduce的总通信时间为 $T_{\text{comm(all-reduce)}} = 2 \times T_{\text{comm(all-gather)}}$。
在大多数公式中,我们将忽略(K-1)/K项,在K ≫ 1的假设下将其近似为1,以简化代数。这产生了一个简单的近似:reduce-scatter时间与每芯片输入的大小成正比,all-gather时间与每芯片输出的大小成正比。
A.2 通信时间计算细节
A.2.1 前馈层,2D权重固定布局
图2(b)显示了分区布局。权重的分区布局为 $E_x F_{yz}$,即它们沿 $d_{\text{model}}$ 维度分成X个分区,沿 $d_{\text{ff}}$ 维度分成Y×Z个分区,其中X×Y×Z = $n_{\text{chips}}$。
我们现在展示如何调整环形的X、Y和Z轴的大小以最小化2D权重固定布局中的总通信时间。通信时间为:
\[T_{\text{comm}} = \frac{2BL}{\text{网络带宽}} \left(\frac{E}{X} + \frac{F}{YZ}\right)\]我们可以在满足可用TPU v4切片形状和X×Y×Z = $n_{\text{chips}}$ 的约束下自由选择X、Y和Z。假设 $d_{\text{ff}} = 4 \times d_{\text{model}}$,我们通过 $X = 0.5 \times \sqrt{n_{\text{chips}}}$ 和 $YZ = 2 \times \sqrt{n_{\text{chips}}}$ 实现最小通信时间。得到的总通信时间为:
\[T_{\text{comm}} = \frac{8BLE}{\sqrt{n_{\text{chips}}} \times \text{网络带宽}}\]A.2.2 前馈层,权重聚集布局
图A.2显示了不同的权重聚集布局,而图2(c)显示了XY权重聚集布局的一个实例。我们选择的特定布局的一个关键方面是权重以与2D权重固定相同的 $E_x F_{yz}$ 布局开始,这样我们可以立即在权重聚集布局和权重固定布局之间切换。就在einsum之前,权重张量在X和Y轴上进行all-gather,通信量为EF/Z。
通过改变X、Y和Z轴的相对大小,我们可以权衡权重通信与激活通信,从而最小化总通信量。我们现在展示权重聚集布局的渐近缩放。设N为权重被all-gather到的芯片数量:在X-权重聚集中N = X,在XY-权重聚集中N = XY,在XYZ-权重聚集中N = XYZ。
权重通信为:
\[T_{\text{comm(weights)}} = \frac{2EF \times N}{n_{\text{chips}} \times \text{网络带宽}}\]激活通信为:
\[T_{\text{comm(acts)}} = \frac{2BLE}{N \times \text{网络带宽}}\]通过选择 $N = \sqrt{BSn_{\text{chips}}/F}$ 来最小化总通信,这产生总通信时间
\[T_{\text{comm}} = \frac{4E\sqrt{BLF}}{\sqrt{n_{\text{chips}}} \times \text{网络带宽}}\]图3显示了随着批次大小增长,通信最优配置如何在这些布局之间切换。虽然2D权重固定策略在每批次token数较低时最小化通信,但不同的权重聚集布局在每批次token数较大时是最优的。
附录 B 最小预填充延迟
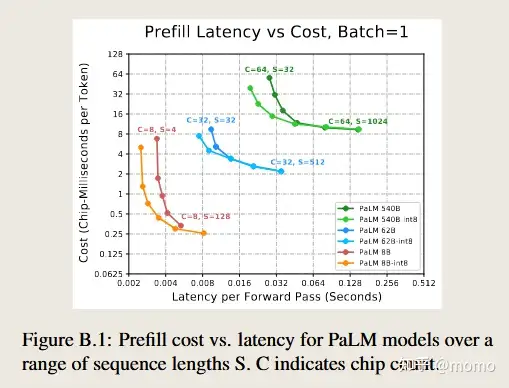
我们在这里报告预填充所需的最小延迟。图B.1显示了当我们在批次大小1下将序列长度从32扫描到1024时,成本与延迟的帕累托前沿。
附录 C MFU与延迟权衡
我们在这里报告模型大小、延迟和MFU之间的关系。图C.1显示了MFU与延迟的帕累托前沿,我们扫描批次大小和芯片数量,与图1相同。解码的MFU通常远低于预填充。在预填充阶段,MFU中的”跳跃”显示了从权重固定2D布局到XYZ权重聚集布局的转换点。
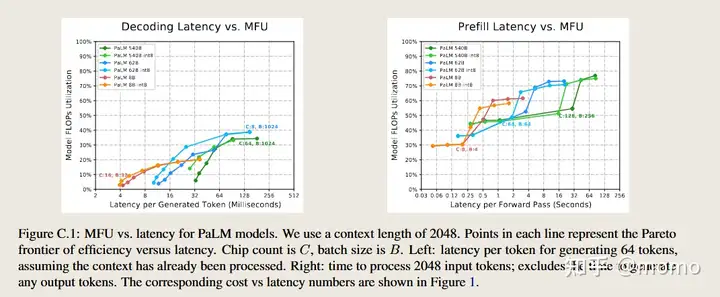
在大多数情况下,较大的模型比较小的模型实现更高的MFU,因为较大的矩阵乘法更高效。然而,在长延迟解码时,PaLM 62B比PaLM 540B实现了更高的MFU,因为前者使用8路模型并行,而后者使用64路模型并行。我们可以通过在高吞吐量(容忍延迟)情况下减少模型并行来进一步优化PaLM 540B。
附录 D 与FASTERTRANSFORMER的完整比较
在本节中,我们报告在64个TPU v4芯片上运行的PaLM 540B模型和Megatron-Turing NLG 530B模型的延迟和MFU,与FasterTransformer基线进行比较。我们首先在表D.1中注意模型架构差异。
然后,我们报告FasterTransformer基准测试中三种配置的完整比较集:20个输入token和8个输出token在表D.2中,60个输入token和20个输出token在表D.3中,128个输入token和8个输出token在表D.4中。
对于每个表,我们用粗体字体报告延迟和MFU的帕累托前沿(跨所有500B级结果的前沿)和下划线(特定于MT-NLG的前沿)。这个前沿不是逐行比较,而是在整个表中全局定义的。它的定义如下:如果对于所有其他基准测试结果(latency₂, MFU₂),要么latency ≤ latency₂,要么MFU ≥ MFU₂(或两者)为真,则基准测试结果(latency, MFU)在帕累托前沿上。在视觉上,这对应于图9中”向上和向左”的位置。
我们不报告低于4的批次大小,因为我们的分区策略在批次上对多查询注意力进行分区,对于小于4的批次大小(TPU v4环形轴的最小大小)不会实现加速。
表D.1:PaLM和Megatron-Turing NLG推理的超参数
| 参数 | PaLM 540B | Megatron 530B |
|---|---|---|
| $n_{\text{params}}$ | 540B | 530B |
| $n_{\text{layers}}$ | 118 | 105 |
| $d_{\text{model}}$ | 18432 | 20480 |
| $d_{\text{ff}}$ | 73728 | 81920 |
| $n_{\text{heads}}$ | 48 | 128 |
| $d_{\text{head}}$ | 256 | 160 |
| 注意力 | 多查询 | 多头 |
| 并行ffn/attn | 是 | 否 |
表D.2:20输入token、8输出token基准测试的结果
所有时间单位为毫秒。粗体和下划线注释不是逐行的,而是显示时间与MFU的帕累托前沿。详见第D节的完整说明。
| batch | FasterTransformer MT-NLG 530B total | 我们的实现 (530B/540B,64个TPU v4,2D分区) | |||||
|---|---|---|---|---|---|---|---|
| TP16 | TP32 | PP3/TP8 | PaLM预填充 | PaLM生成 | PaLM总计 | MT-NLG总计 | |
| time/MFU | time/MFU | time/MFU | time/MFU | time/MFU | time/MFU | time/MFU | |
| 1 | 565/1% | 431/1% | 842/0% | - | - | - | - |
| 2 | 598/2% | 455/1% | 860/1% | - | - | - | - |
| 4 | 616/4% | 493/2% | 867/2% | 34/14% | 255/1% | 289/2% | 289/2% |
| 8 | 660/7% | 523/5% | 929/3% | 40/25% | 226/2% | 265/5% | 304/4% |
| 16 | 730/13% | 575/8% | 1049/6% | 58/34% | 234/3% | 292/9% | 339/8% |
| 32 | 865/22% | 672/14% | 1283/10% | 99/40% | 235/7% | 334/16% | 420/13% |
| 64 | 1191/32% | 942/20% | 1722/15% | 186/42% | 265/12% | 451/24% | 532/20% |
| 128 | 1862/41% | 1431/27% | 2124/24% | 356/44% | 312/20% | 668/33% | 740/29% |
| 256 | 3341/46% | 2483/31% | 3140/32% | 668/47% | 415/30% | 1083/41% | 1151/38% |
| 512 | - | - | - | 1366/46% | 671/37% | 2037/43% | 2151/40% |
| 1024 | - | - | - | 2785/45% | 1257/40% | 4041/44% | 4082/42% |
表D.3:60输入token、20输出token基准测试的结果
所有时间单位为毫秒。粗体和下划线注释不是逐行的,而是显示时间与MFU的帕累托前沿。详见第D节的完整说明。
| batch | FasterTransformer MT-NLG 530B total | 我们的实现 (530B/540B,64个TPU v4,2D分区) | |||||
|---|---|---|---|---|---|---|---|
| TP16 | TP32 | PP3/TP8 | PaLM预填充 | PaLM生成 | PaLM总计 | MT-NLG总计 | |
| time/MFU | time/MFU | time/MFU | time/MFU | time/MFU | time/MFU | time/MFU | |
| 1 | 1379/1% | 1037/1% | 2085/1% | - | - | - | - |
| 2 | 1515/2% | 1110/2% | 2122/1% | - | - | - | - |
| 4 | 1512/4% | 1198/3% | 2184/2% | 50/29% | 640/1% | 690/3% | 678/3% |
| 8 | 1631/8% | 1295/5% | 2367/4% | 80/37% | 574/2% | 653/6% | 728/5% |
| 16 | 1868/15% | 1454/9% | 2753/7% | 153/39% | 602/3% | 755/10% | 838/9% |
| 32 | 2361/23% | 1804/15% | 3543/10% | 270/44% | 626/6% | 896/18% | 1058/15% |
| 64 | 3383/32% | 2646/21% | 4117/18% | 501/47% | 717/11% | 1218/26% | 1275/24% |
| 128 | 5406/40% | 4099/27% | 5319/27% | 985/48% | 829/19% | 1814/35% | 1902/32% |
| 256 | OOM | 7203/30% | 8318/35% | 2041/46% | 1114/28% | 3155/40% | 3189/39% |
| 512 | - | - | - | 4167/45% | 1743/36% | 5910/43% | 6210/40% |
| 1024 | - | - | - | 8349/45% | 3260/39% | 11608/43% | 12390/40% |
表D.4:128输入token、8输出token基准测试的结果
所有时间单位为毫秒。粗体和下划线注释不是逐行的,而是显示时间与MFU的帕累托前沿。详见第D节的完整说明。
| batch | FasterTransformer MT-NLG 530B total | 我们的实现 (530B/540B,64个TPU v4,2D分区) | |||||
|---|---|---|---|---|---|---|---|
| TP16 | TP32 | PP3/TP8 | PaLM预填充 | PaLM生成 | PaLM总计 | MT-NLG总计 | |
| time/MFU | time/MFU | time/MFU | time/MFU | time/MFU | time/MFU | time/MFU | |
| 1 | 585/5% | 451/3% | 866/2% | - | - | - | - |
| 2 | 667/9% | 508/6% | 932/4% | - | - | - | - |
| 4 | 765/15% | 606/10% | 1097/7% | 81/39% | 258/1% | 343/10% | 338/10% |
| 8 | 990/23% | 766/15% | 1434/11% | 149/42% | 234/2% | 403/17% | 384/16% |
| 16 | 1377/34% | 1074/22% | 2104/15% | 287/44% | 253/3% | 586/23% | 540/23% |
| 32 | 2251/41% | 1741/27% | 2623/23% | 536/47% | 263/6% | 796/34% | 799/33% |
| 64 | 4002/46% | 3114/30% | 3578/34% | 1056/48% | 317/10% | 1329/40% | 1372/39% |
| 128 | OOM | 5784/32% | 5512/45% | 2202/46% | 381/17% | 2343/46% | 2583/45% |
| 256 | OOM | 11232/33% | 9614/51% | 4479/45% | 431/29% | 4710/45% | 4911/45% |
| 512 | - | - | - | 8913/45% | 734/34% | 9673/44% | 9647/43% |
| 1024 | - | - | - | 17766/45% | 1370/37% | 19723/43% | 19136/43% |
评论