在深度学习领域,Transformer模型和自注意力机制(Attention)已经成为支撑自然语言处理、计算机视觉和其他领域的重要基石。随着模型规模的扩大,计算复杂度和内存需求也随之呈指数级增长,尤其是自注意力机制中的计算和存储需求。因此,如何高效地计算自注意力成为了深度学习编译器和硬件加速器优化的核心课题之一。
FlashAttention是一种为解决这一问题而提出的高效计算方法,它在保持计算精度的同时,大幅度减少了内存访问并提高了计算速度。FlashAttention通过引入一系列优化策略,包括内存布局、分块(Tiling)和调度(Tuning)等手段,有效地提升了自注意力机制的性能。在本文中,我们将从AI编译器的角度出发,深入分析FlashAttention的工作原理以及它如何通过编译器优化手段来实现性能提升。
ai编译器
在深度学习编译器中,优化技术可分为两大类:前端优化 和 后端优化。前端优化主要关注计算图的结构优化,而后端优化则针对具体硬件进行性能调优。
前端优化
在深度学习编译器的前端部分,计算图(IR,Intermediate Representation)经过一系列优化,以提高计算效率和减少冗余。前端优化通常在硬件无关的层面进行,即优化仅基于计算图的结构,并不依赖于具体的硬件实现。前端优化可分为三个主要类别:
节点级优化
节点级优化关注于对单一操作节点的优化。常见的节点级优化包括:
- 空操作消除(Nop Elimination):移除不进行任何实际计算的操作节点,例如输入不足的操作。
- 零维张量消除(Zero-dim-tensor Elimination):去除输入为零维张量的无效操作,减少不必要的计算。
- 常量折叠(Constant Folding):用常量表达式的计算结果替换节点中的常量操作。
这些优化有助于减少不必要的计算,并提高图的计算密度。
块级优化
块级优化对计算图中的多个节点进行联合优化,常见的块级优化技术包括:
- 代数化简(Algebraic Simplification):简化数学表达式,利用代数恒等式(如 x \times 1 = x)减少计算量。
- 算子融合(Operator Fusion):将多个操作融合成一个操作,从而减少内存访问和中间计算结果的存储。例如,将矩阵乘法与加法操作融合为一个复合操作,减少内存访问。
- 矩阵转置优化(Transpose Optimization):优化矩阵转置操作,减少不必要的转置节点。
这些优化通常涉及对相邻操作节点的重排,以减少冗余计算,并提高执行效率。
数据流级优化
数据流级优化聚焦于全局优化,例如:
- 公共子表达式消除(Common Sub-expression Elimination, CSE):避免重复计算相同的子表达式。
- 死代码消除(Dead Code Elimination, DCE):移除不会被使用的计算或结果,减少无用计算的浪费。
这些优化技术可以在整个计算图范围内去除冗余,减少计算量并提高性能。
后端优化:分块与调度
分块(Tiling)
在深度学习模型的计算过程中,矩阵乘法是一个计算密集型操作,尤其是在自注意力机制(如 Transformer)中,计算复杂度通常为 O(n^2),这使得长序列的计算变得非常缓慢。分块(Tiling) 优化技术通过将计算任务分成更小的块(tile),让计算可以在更小的区域内进行,进而提高内存局部性并优化并行计算。对于深度学习编译器来说,分块有以下优势:
- 提高缓存效率:通过在更小的块上进行计算,数据可以被更有效地缓存和重用,减少内存访问。
- 并行计算:每个计算块可以并行执行,从而提升计算吞吐量。
在 FlashAttention 中,分块被广泛应用于矩阵乘法操作中,通过将大矩阵分成小块,能够在多个计算单元上并行处理数据,从而加速 Attention 计算。
调度(Tuning)
调度是对计算图中的计算任务进行合理排序和优化安排的过程。良好的调度能够提高硬件资源的利用率,减少内存带宽瓶颈,并提高计算吞吐量。调度技术包括:
- 内存访问优化:通过优化内存访问模式,避免频繁的内存读取和写入,从而减少延迟。
- 并行化和向量化:将计算任务分配到多个计算单元上,并通过向量化技术提高每个计算单元的工作负载。
- 循环优化:如循环展开(Loop Unrolling)和循环重排序(Loop Reordering),用于提高内存局部性和计算效率。
FlashAttention 利用这些调度技术,特别是通过优化计算任务的执行顺序和内存访问模式,使得 Attention 计算在 GPU 上得以高效执行。通过分块和调度的结合,FlashAttention 能够显著减少内存占用和计算延迟。
FlashAttention
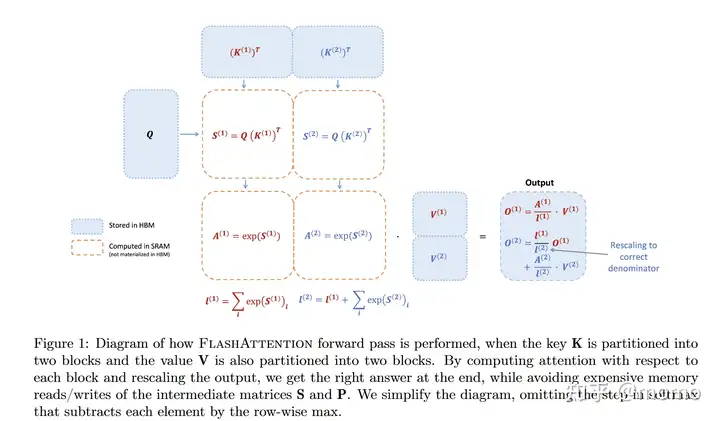
FlashAttention的计算如上图所示,将原有的矩阵(shape为 $N \times d$)切分为小的矩阵(具体shape为 $Q: T_r \times d$,$K: T_c \times d$,$V: T_c \times d$,$O: T_r \times d$)。外层循环遍历Q,内层循环遍历KV,分块计算O,最后更新O矩阵。这就是ai编译器中的分块(Tiling)和调度(Tuning)的概念。使用这个方法,可以充分利用gpu的SRAM。从而能够提高attention的计算效率。
不过和ai编译器不同的是,ai编译器一般是写一些优化代码(pass),将原有的模型优化成为新的模型,FlashAttention是直接写出优化后的kernel,然后替代原有的kernel。这是因为llm的模型结构相对比较单一,不需要进行变换,直接对kernel做优化就可以了。
FlashAttention 还做了内核融合优化,使得不需要从cpu和gpu之间频繁的传递数据,这也是能够加快的关键。
Online Softmax 核心思想
Online softmax 允许我们在看到数据流的过程中增量式地计算 softmax,无需存储所有数据。
数值稳定的 Softmax
为了数值稳定,softmax 通常这样计算:
\[\text{softmax}(\mathbf{x})_i = \frac{e^{x_i - m}}{\sum_j e^{x_j - m}}\]其中 $m = \max_j x_j$ 是最大值。
关键统计量
对于每一行,我们需要维护:
- $m $:行最大值
- $\ell $:归一化因子(分母)$\ell = \sum_j e^{x_j - m} $
两块情况的完整推导
假设我们将 $\mathbf{K} $ 和 $\mathbf{V} $ 分成两个块:$\mathbf{K} = [\mathbf{K}^{(1)}, \mathbf{K}^{(2)}] $,$\mathbf{V} = [\mathbf{V}^{(1)}, \mathbf{V}^{(2)}] $。
第一个块的处理
步骤 1:计算注意力分数
\[\mathbf{S}^{(1)} = \mathbf{Q}(\mathbf{K}^{(1)})^T \in \mathbb{R}^{B_r \times B_c}\]步骤 2:计算行最大值
\[m^{(1)} = \text{rowmax}(\mathbf{S}^{(1)}) \in \mathbb{R}^{B_r}\]步骤 3:计算归一化因子(基于 $m^{(1)}$ )
\[\ell^{(1)} = \text{rowsum}(e^{\mathbf{S}^{(1)}-m^{(1)}}) \in \mathbb{R}^{B_r}\]步骤 4:计算部分输出(未归一化)
\[\tilde{\mathbf{O}}^{(1)} = e^{\mathbf{S}^{(1)}-m^{(1)}}\mathbf{V}^{(1)} \in \mathbb{R}^{B_r \times d}\]注意:$\tilde{\mathbf{O}}^{(1)}$ 此时还不是正确的输出,因为归一化因子是基于部分数据计算的。
第二个块的处理
步骤 5:更新全局最大值
\[m^{(2)} = \max(m^{(1)}, \text{rowmax}(\mathbf{S}^{(2)})) = m\]这是真实的全局最大值。
步骤 6:更新归一化因子
由于最大值从 $m^{(1)}$ 变为 $m^{(2)}$ ,需要重新缩放之前的归一化因子:
\[\begin{align} \ell^{(2)} &= e^{m^{(1)}-m^{(2)}} \ell^{(1)} + \text{rowsum}(e^{\mathbf{S}^{(2)}-m^{(2)}}) \\ &= \text{rowsum}(e^{\mathbf{S}^{(1)}-m}) + \text{rowsum}(e^{\mathbf{S}^{(2)}-m}) \\ &= \ell \end{align}\]推导说明:
$\ell^{(1)} = \sum_j e^{S^{(1)}_{ij} - m^{(1)}} $
基于新的最大值应该是:
\[\sum_j e^{S^{(1)}_{ij} - m^{(2)}} = e^{m^{(1)}-m^{(2)}} \sum_j e^{S^{(1)}_{ij} - m^{(1)}} = e^{m^{(1)}-m^{(2)}} \ell^{(1)}\]步骤 7:更新输出(未归一化)
同样需要重新缩放 $\tilde{\mathbf{O}}^{(1)}$ :
\[\begin{align} \tilde{\mathbf{O}}^{(2)} &= \text{diag}(e^{m^{(1)}-m^{(2)}})\tilde{\mathbf{O}}^{(1)} + e^{\mathbf{S}^{(2)}-m^{(2)}}\mathbf{V}^{(2)} \\ &= e^{\mathbf{S}^{(1)}-m}\mathbf{V}^{(1)} + e^{\mathbf{S}^{(2)}-m}\mathbf{V}^{(2)} \end{align}\]推导说明:
$\tilde{\mathbf{O}}^{(1)} = e^{\mathbf{S}^{(1)}-m^{(1)}}\mathbf{V}^{(1)} $
基于新的最大值应该是:
\[e^{\mathbf{S}^{(1)}-m^{(2)}}\mathbf{V}^{(1)} = e^{m^{(1)}-m^{(2)}} e^{\mathbf{S}^{(1)}-m^{(1)}}\mathbf{V}^{(1)} = e^{m^{(1)}-m^{(2)}} \tilde{\mathbf{O}}^{(1)}\]步骤 8:最终归一化
\[\mathbf{O}^{(2)} = \text{diag}(\ell^{(2)})^{-1}\tilde{\mathbf{O}}^{(2)} = \mathbf{O}\]这就是最终正确的注意力输出!
Attention 前向和反向传播公式
前向传播 (Forward Pass)
输入
- $\mathbf{Q} \in \mathbb{R}^{N \times d} $ (Query)
- $\mathbf{K} \in \mathbb{R}^{N \times d} $ (Key)
- $\mathbf{V} \in \mathbb{R}^{N \times d} $ (Value)
计算过程
\[\mathbf{S} = \mathbf{Q}\mathbf{K}^T \in \mathbb{R}^{N \times N}\] \[\mathbf{P} = \text{softmax}(\mathbf{S}) \in \mathbb{R}^{N \times N}\] \[\mathbf{O} = \mathbf{P}\mathbf{V} \in \mathbb{R}^{N \times d}\]反向传播 (Backward Pass)
输入
- $\frac{\partial L}{\partial \mathbf{O}} \in \mathbb{R}^{N \times d} $ (输出梯度)
- $\mathbf{Q}, \mathbf{K}, \mathbf{V} $ (前向传播时的输入)
- $\mathbf{P} $ (前向传播时的注意力权重)
计算过程
1. 对 V 的梯度:
\[\frac{\partial L}{\partial \mathbf{V}} = \mathbf{P}^T \frac{\partial L}{\partial \mathbf{O}} \in \mathbb{R}^{N \times d}\]2. 对 P 的梯度:
\[\frac{\partial L}{\partial \mathbf{P}} = \frac{\partial L}{\partial \mathbf{O}} \mathbf{V}^T \in \mathbb{R}^{N \times N}\]3. 对 S 的梯度(softmax 反向传播):
\[\frac{\partial L}{\partial \mathbf{S}} = \mathbf{P} \odot \left(\frac{\partial L}{\partial \mathbf{P}} - \text{diag}\left(\frac{\partial L}{\partial \mathbf{P}} \mathbf{P}^T\right)\right) \in \mathbb{R}^{N \times N}\]或者简化为:
\[\frac{\partial L}{\partial S_{ij}} = P_{ij}\left(\frac{\partial L}{\partial P_{ij}} - \sum_k \frac{\partial L}{\partial P_{ik}} P_{ik}\right)\]4. 对 Q 的梯度:
\[\frac{\partial L}{\partial \mathbf{Q}} = \frac{\partial L}{\partial \mathbf{S}} \mathbf{K} \in \mathbb{R}^{N \times d}\]5. 对 K 的梯度:
\[\frac{\partial L}{\partial \mathbf{K}} = \left(\frac{\partial L}{\partial \mathbf{S}}\right)^T \mathbf{Q} \in \mathbb{R}^{N \times d}\]反向传播由于不保存P,所以需要重新计算:
在标准 attention 中,反向传播需要用到注意力权重 $\mathbf{P}$ :
\[\frac{\partial L}{\partial \mathbf{S}} = \mathbf{P} \odot \left(\frac{\partial L}{\partial \mathbf{P}} - \text{diag}\left(\frac{\partial L}{\partial \mathbf{P}} \mathbf{P}^T\right)\right)\]但 FlashAttention 不保存 $\mathbf{P}$ (太大了),所以需要在反向传播时重新计算 $\mathbf{P}$ 。
重新计算 P 需要 logsumexp
要重新计算 $\mathbf{P}$ ,需要:
\[\mathbf{P} = \text{softmax}(\mathbf{S}) = \frac{e^{\mathbf{S} - m}}{\ell}\]其中:
- $m = \text{rowmax}(\mathbf{S})$ :可以重新计算
- $\ell = \sum_j e^{S_{ij} - m}$ :这就是归一化因子
为什么保存 logsumexp 而不是 $\ell$ ?
数值稳定性!保存 $L = m + \log(\ell) = m + \log\left(\sum_j e^{S_{ij} - m}\right)$
这样在反向传播时:
\[\mathbf{P}_{ij} = \frac{e^{S_{ij} - m}}{\ell} = \frac{e^{S_{ij} - m}}{e^{L - m}} = e^{S_{ij} - L}\]优势:
- 避免指数运算的数值溢出
- $L$ 是对数空间的值,数值范围更稳定
- 可以直接用 $e^{S_{ij} - L}$ 计算 $P_{ij}$
算法伪代码
设置块大小:
\[B_c = \left\lceil \frac{M}{4d} \right\rceil, \quad B_r = \min\left(\left\lceil \frac{M}{4d} \right\rceil, d\right)\]其中:
- $M $ 是 SRAM 的大小(以元素数量计)
- $d $ 是注意力头的维度
- $B_c $ 是列块大小(Key/Value 的序列长度方向)
- $B_r $ 是行块大小(Query 的序列长度方向)
参数说明
$B_c = \left\lceil \frac{M}{4d} \right\rceil$
列块大小的选择考虑了 SRAM 容量限制:
- 需要存储 $\mathbf{K}^{(j)} \in \mathbb{R}^{B_c \times d} $
- 需要存储 $\mathbf{V}^{(j)} \in \mathbb{R}^{B_c \times d} $
- 需要存储 $\mathbf{Q}^{(i)} \in \mathbb{R}^{B_r \times d} $
- 需要存储 $\mathbf{S}^{(i,j)} \in \mathbb{R}^{B_r \times B_c} $
总内存使用约为 $2B_c d + B_r d + B_r B_c $,当 $B_r \approx B_c $ 时,主要项为 $4B_c d $,因此 $B_c \approx \frac{M}{4d} $。
$B_r = \min\left(\left\lceil \frac{M}{4d} \right\rceil, d\right)$
行块大小的选择有两个约束:
- 内存约束:$B_r $ 不能太大,否则超出 SRAM 容量,因此 $B_r \leq \frac{M}{4d} $
- 维度约束:$B_r $ 不需要超过头维度 $d $,因为计算效率会受限
因此取两者的最小值。
forward

backward

附:数值稳定的logsumexp(L)推导
步骤 1:原始的 logsumexp 定义
\[L_i = \log\left(\sum_j e^{S_{ij}}\right)\]步骤 2:定义行最大值
\[m_i = \max_j S_{ij}\]步骤 3:在求和中巧妙地乘以和除以 $e^{m_i}$
\[L_i = \log\left(\sum_j e^{S_{ij}} \cdot \frac{e^{m_i}}{e^{m_i}}\right)\]步骤 4:提取 $e^{m_i}$ 到求和外面
\[L_i = \log\left(e^{m_i} \cdot \sum_j \frac{e^{S_{ij}}}{e^{m_i}}\right)\]步骤 5:使用对数的乘法法则 $\log(ab) = \log(a) + \log(b)$
\[L_i = \log(e^{m_i}) + \log\left(\sum_j \frac{e^{S_{ij}}}{e^{m_i}}\right)\]步骤 6:简化 $\log(e^{m_i}) = m_i$
\[L_i = m_i + \log\left(\sum_j \frac{e^{S_{ij}}}{e^{m_i}}\right)\]步骤 7:使用指数的除法法则 $\frac{e^a}{e^b} = e^{a-b}$
\[L_i = m_i + \log\left(\sum_j e^{S_{ij} - m_i}\right)\]步骤 8:定义 $\ell_i = \sum_j e^{S_{ij} - m_i}$ (归一化因子)
最终得到:
\[\boxed{L_i = m_i + \log(\ell_i) = m_i + \log\left(\sum_j e^{S_{ij} - m_i}\right)}\]关系总结
\[\begin{align} m_i &= \max_j S_{ij} \\ \ell_i &= \sum_j e^{S_{ij} - m_i} \\ L_i &= m_i + \log(\ell_i) \end{align}\]或者写成完整形式:
\[L_i = \log\left(\sum_j e^{S_{ij}}\right) = m_i + \log\left(\sum_j e^{S_{ij} - m_i}\right)\]
评论